Radiohalos

Proceedings of the 63rd Annual Meeting of the Pacific Division, American Association for the Advancement of Science 1, 38 (1984).

If the earth was created, it is axiomatic that created (primordial) rocks must now exist on the earth, and if there was a Flood there must now exist sedimentary rocks and other evidences of that event. But, if the general uniformitarian principle is correct, the universe evolved to its present state only by the unvarying action of known physical laws and all natural phenomena must fit into the evolutionary mosaic. If this fundamental principle is wrong, all the pieces in the evolutionary mosaic become unglued. Evidence that something is drastically wrong comes from the fact that this basic evolutionary premise has failed to provide a verifiable explanation for the widespread occurrence of Po halos in Precambrian granites, a phenomena which I suggest are in situ evidences that those rocks were created almost instantaneously in accord with Psalm 33:6,9: "By the word of the Lord were the heavens made; and all the host of them by the breath of his mouth. For he spake, and it was done; he commanded, and it stood fast." I have challenged my colleagues to synthesize a piece of granite with ²¹⁸Po halos as a means of falsifying this interpretation, but have not received a response. It is logical that this synthesis should be possible if the uniformitarian principle is true. Underdeveloped U halos in coalified wood having high U/Pb ratios are cited evidences for a Flood-related recent (within the past few thousand years) emplacement of geological formations thought to be more than 100,000,000 years old. Results of differential He analyses of zircons taken from deep granite cores are evidence for a recently created, several-thousand-year-age of the earth. A creation model with three singularities, involving events beyond explanation by known physical laws, is proposed to account for these evidences. The first singularity is the ex nihilo creation of our galaxy nearly 6000 years ago. Finally, a new model for the structure of the universe is proposed based on the idea that all galaxies, including the Milky Way, are revolving about the Center of the universe, which from Psalm 103:19 I equate with the fixed location of God's throne. This model requires an absolute reference frame in the universe whereas modern Big Bang cosmology mandates there is no Center (the Cosmological Principle) and no absolute reference frame (the theory of relativity). The motion of the solar system through the cosmic microwave radiation is cited as unequivocal evidence for the existence of an absolute reference frame.

[* Current Address: P.O. Box 12067, Knoxville, TN 37912]

[Larger picture] Figure 1. The scale for all photomicrographs is 1 cm = 25.0 μm, except for (h') and (r'), which are enlargements of (h) and (r). (a) Schematic drawing of 238U halo with radii proportional to ranges of alpha particles in air. (b) Schematic of 210Po halo. [(c) Schematic of 214Po halo. (d) Schematic of 218Po halo.] (e) Coloration band formed in mica by 7.7-Mev 4He ions. Arrow shows direction of beam penetration. (f) A 238U halo in biotite formed by sequential α-decay of the 238U decay series. (g) Embryonic 238U halo in fluorite with only two rings developed. (h) Normally developed 238U halo in fluorite with nearly all rings visible. (h') Same halo as in (h) but at higher magnification. (i) Well-developed 238U halo in fluorite with slightly blurred rings. (j) Overexposed 238U halo in fluorite, showing inner ring obliteration. (k) Two overexposed 238U halos in fluorite, showing outer ring reversal effects. [(l) More overexposed 238U halo in fluorite, showing outer ring reversal effects.] (m) Second-stage reversal in a 238U halo in fluorite. The ring sizes are unrelated to 238U alpha particle ranges. (n) Three 210Po halos of light, medium, and very dark coloration in biotite. Note the difference in radius. (o) Three 210Po halos of varying degrees of coloration in fluorite. (p) A 214Po halo in biotite. (q) Two 218Po halos in biotite. (r) Two 218Po halos in fluorite. (r') Same halos as in (r) but at higher magnification. (Reprinted from ref. (2) by permission of the AAAS.)

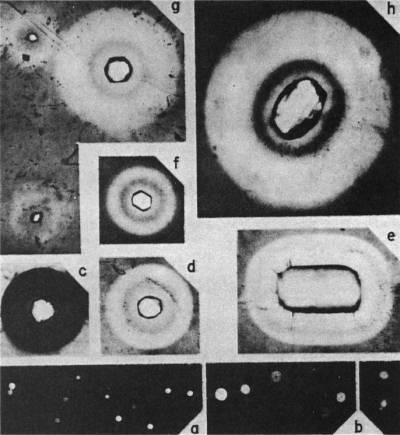
Figure 2. The scale for all photographs is 1 cm = 25 μm. (a) Dwarf halos (≃2 μm radius) in Ytterby mica. (b) Dwarf halos (3 μm < r < 9 μm) in Ytterby mica. (c) Overexposed Th halo in ordinary biotite. (d) Th halo in Madagascan mica. (e) Th halo in Madagascan mica with a larger inclusion. (f) U halo in Madagascan mica. (g) Giant halo of ≃65 μm radius, and two light Th halos (Madagascan mica). (h) Giant halo of ≃90 μm radius Madagascan mica. (Reprinted from ref. (1) by permission of the ARNS.)

Uranium and Thorium Radiohalos in Minerals

A radioactive halo is generally defined as any type of discolored, radiation-damaged region within a mineral and usually results from either alpha or, more rarely, beta emission from a central radioactive inclusion. When the central inclusions, or radiocenters, are small (1 μm), the U and Th daughter alpha emitters produce a series of discolored concentric spheres, which in thin section appear microscopically as concentric rings whose radii correspond to the ranges of the various alpha emitters in the mineral.

Ordinary radiohalos are herein defined as those which initiate with ²³⁸U and/or ²³²Th alpha decay (1), irrespective of whether the actual U or Th halo closely matches the respective idealized alpha decay patterns. In a few instances the match is very good.

Compare, for example, the idealized U halo ring pattern in Fig. 1a with the well developed U halos in biotite (Fig. 1f) and fluorite (Fig. 1h,h'); these halos have ring sizes that agree very well (1,2) with the ⁴He ion accelerator-induced coloration bands in these minerals (see Table 1). In general a halo ring can be assigned to a definite alpha emitter with confidence only when the halo radiocenter is about 1 μm in size.

In other cases, however, such as the halos in fluorite (1,2) shown in Fig. 1(g, i-m), much work was required before these halos could be reliably associated with U alpha decay (2). As explained elsewhere (2), reversal effects accompanying extreme radiation damage caused the appearance of rings that could not be associated with definite alpha emitters of the U decay chain. Thus some halos may exhibit a ring structure different from the idealized U and/or Th alpha decay patterns because of reversal effects. And even though most other halos exhibit blurred ring structures due to the large size of the inclusions, nevertheless the outer dimensions allow them to be classified as U and/or Th types.

Modern analytical techniques such as Scanning Electron Microscope X Ray Fluoresence (SEMXRF) and Ion Microprobe Mass Spectrometry (IMMA) methods have been utilized to show that U and Th and their respective end-product isotopes of Pb are contained within the U and Th halo radiocenters. As is noted shortly, these modern analytical techniques have proved quite valuable in demonstrating that Po halo radiocenters in minerals contain little or no U or Th, which is in direct contrast to the abundance of these elements detected in the U and/or Th halo radiocenters (2,3).

Radioactive Halos and the Question of Invariant Decay Rates

A most important question pertaining to the evolution/creation issue is whether radioactive decay rates have remained invariant during the course of earth history. If they have, geochronologists are justified in interpreting various parent/daughter isotope ratios found in undisturbed rocks in terms of elapsed time. If on the other hand there have been periods in earth history where the decay rate was higher (i.e., during a singularity), then in general the isotope ratios in rocks would not reflect elapsed time except in the specific case where secondary rocks or substances containing only the parent radio-nuclide formed at the end of the most recent singularity. The practical significance of this last statement will be evident in the discussion of the secondary, U halos found in coalified wood specimens from the Colorado Plateau.

Even though most of Joly's (4) measurements of U and Th halos showed their radii were about the sizes expected from the alpha decay energies of the U and Th decay chains, nevertheless he claimed there were slight discrepancies which raised questions about whether the radioactive decay rate had been constant over geological time. His result was not confirmed however by later halo radii measurements (5-10), which agreed to within experimental error with the theoretical sizes. To eliminate any uncertainty about this correspondence I irradiated specimens of various minerals with He ion beams of varying energies to produce different size coloration bands whose widths corresponded to the various alpha energies of the U decay chain. The results of these experiments, presented in Table 1, show there is excellent agreement between the U and Th halo radii and equivalent He ion produced penetration depths (2).

The basis for thinking that standard size U and Th halos imply an invariant decay rate throughout geological time proceeds from the quantum mechanical treatment of alpha decay, which in general shows that the probability for alpha decay for a given nuclide is dependent on the energy with which the alpha particle is emitted from the nucleus. The argument is that if the decay rate had varied in the past, then the U and Th halo rings would be of different size now because the energies of the alpha particles would have been different during the period of change. This argument assumes that a change in the decay rate must necessarily be explainable by quantum mechanics, which is of course an integral part of the uniformitarian framework. Thus, the usual proof of decay rate invariance based on standard size U and Th halos is nothing more than a circular argument which assumes the general uniformitarian principle is correct. In fact, the failure of the uniformitarian principle to explain the evidence for creation presented herein invalidates the basis for the above proof.

Polonium, Dwarf, and Giant Halos in Minerals

Of the three types of unusual halos that appear distinct from those formed by U and/or Th alpha decay, only the Po halos, Fig.1 (b-d, n-r, r'), can presently be identified with known alpha radioactivity (1-3,11-13). Po halos occupy a special niche in my creation model, and these halos will be discussed in more detail subsequently. Several lines of evidence which indicate the enigmatic dwarf halos (see Fig. 2) were produced by some presently unidentified radioactivity have been summarized (1,12,14,15). The rapid etch from HF and the K/Ca inversion are strongly characteristic of highly radiation-damaged regions.

The characteristics of the giant halos found in a certain Madagascan mica have also been summarized (1,14,16), and while no definitive evidence as yet exists for a radioactive origin, some halos with opaque inclusions in this same mica exhibit isotopic anomalies which raise questions about the uniformity of U and Th alpha decay. For example, the mass scans and x-ray fluorescence analyses shown in Fig. 3 clearly indicate that, whereas both the monazite and opaque inclusions exhibit ²⁰⁶Pb and ²⁰⁷Pb from U decay, the opaque inclusions exhibit a marked deficiency of ²⁰⁸Pb from ²³²Th decay (14).

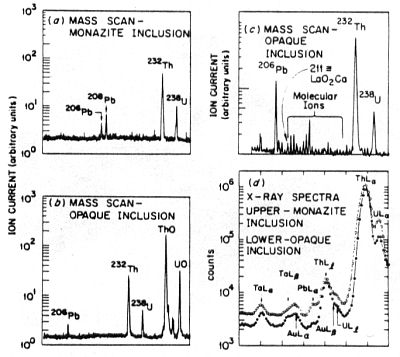
Figure 3. Mass scans and an x-ray fluorescence spectrum of a monazite and an opaque halo inclusion in Madagascan mica, showing Pb deficiency in the latter.

Secondary Radiohalos in Coalified Wood

All the various types of halos discussed thus far are termed primary halos because they developed from alpha radioactivity emanating from small accessory inclusions that were present when the mineral crystallized. But secondary halos also exist in pieces of coalified wood taken from highly uraniferous deposits in the Colorado Plateau. There is abundant evidence that U solutions infiltrated much of the sedimentary material in the geological formations of that region when the wood was still in a gel-like condition (17). When U-bearing solutions passed through pieces of wood, certain active sites within these specimens preferentially collected U, other sites collected rare earth type elements, and still others Se, Po, and Pb. It is quite significant that the U halos, which developed around the tiny U-rich sites, are all underdeveloped, which, on the basis of a uniform decay rate (the rationale for using this assumption for these specimens will be explained subsequently), suggests only a relatively short time since U infiltration. Ion microprobe mass scans of these U halo centers have shown extremely high ²³⁸U/²⁰⁶Pb ratios, which, again on the assumption of a uniform decay rate, is consistent with a U infiltration within the last several thousand years (17).

Figure 4. Elliptical (compressed) 210Po halos in coalified wood from the Colorado Plateau. Reproduced from ref. (17) by permission of the AAAS. (× 250)

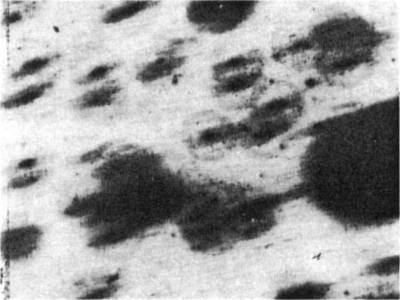
Figure 5. Circular 210Po halos in Colorado Plateau coalified wood. (× 250)

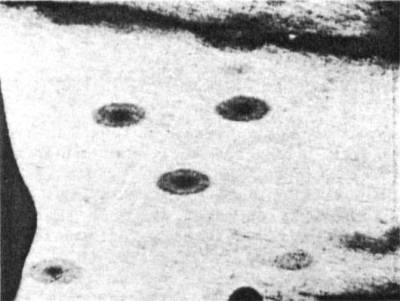
Figure 6. Circular and elliptical 210Po halo in Colorado Plateau coalified wood. Reproduced from ref. (17) with AAAS permission. (× 250)

Similar underdeveloped U halos have been found in the coalified wood from the Chattanooga Shale, and in fact recent ion microprobe analyses show, in agreement with earlier results (17), that the ²³⁸U/²⁰⁶Pb ratios of the U halos in the Colorado Plateau samples (Eocene, Triassic, and Jurassic) and the Chattanooga Shale (Devonian) are virtually indistinguishable. These results suggest that U-infiltration occurred concurrently in all these formations.

Another class of more sharply defined halos was also discovered in the Colorado Plateau coalified wood specimens (17). The centers of these halos exhibit a distinct metallic-like reflectance when viewed with reflected light. Three different varieties of this halo exist: one with a circular cross section, another with an elliptical cross section with variable major and minor axes, and a third most unusual one that is actually a dual halo, being a composite of a circular and an elliptical halo around exactly the same radio-center (see Figs. 4-6).

Although the elliptical halos differ radically from the circular halos in minerals, the circular type resembles the ²¹⁰Po halo in minerals and variations in the radii of circular halos approximate the calculated penetrated distances (26 to 31 μm) of the ²¹⁰Po alpha particle (energy E = 5.3 MeV) in this coalified wood (17). Henderson (18) theorized that Po halos might form in minerals when U-daughter Po isotopes or their alpha precursors were preferentially accumulated into small inclusions from some nearby U source. This hypothesis has not been confirmed for the origin of three distinct types of Po halos in U-poor minerals (1,2,11), but it does seem to provide a reasonable explanation for the origin of ²¹⁰Po halos in U-rich coalified wood specimens.

Electron microscope x-ray fluorescence analyses showed these halo centers were mainly Pb and Se. This composition fits well into the secondary accumulation hypothesis for both of the U-daughters, ²¹⁰Po (half-life, t_½ = 138 days) and its beta precursor ²¹⁰Pb (t_½ = 22 y), possess the two characteristics that are vitally essential for the hypothesis: (i) chemical similarity with the elements in the inclusion and (ii) half-lives sufficiently long to permit accumulation prior to decay, a requirement related to the nuclide transport rate.

What is the meaning of the ²¹⁰Po halos in Figs. 4-6? Clearly, the variations in shape can be attributed to plastic deformation which occurred prior to coalification. Since the model for ²¹⁰Po formation thus envisions that both ²¹⁰Po and ²¹⁰Pb were accumulating simultaneously in the Pb-Se inclusion, a spherical ²¹⁰Po halo could develop in 0.5 to 1 year from the ²¹⁰Po atoms initially present and a second similar ²¹⁰Po halo could develop in 25 to 50 years as the ²¹⁰Pb atoms more slowly beta decayed to produce another crop of ²¹⁰Po atoms. If there was no deformation of the matrix between these periods, the two ²¹⁰Po halos would simply coincide. If, however, the matrix was deformed between the two periods of halo formation, then the first halo would have been compressed into an ellipsoid, and the second would be a normal sphere. The result would be a dual "halo" (Fig. 6). The widespread occurrence of these dual halos in both Triassic and Jurassic specimens can actually be considered corroborative evidence for a one-time introduction of U into these formations, because it is then possible to account for their structure on the basis of a single specifically timed tectonic event (17).

Halos in Coalified Wood: a Flood-Related Phenonena

A worldwide Flood, which is postulated to have occurred about 1650 years after creation, is the third singularity in the creation model proposed herein. I have advanced the hypothesis that the underdeveloped U halos in both the Colorado Plateau and Chattanooga Shale coalified wood specimens exhibit very high U/Pb ratios because the uranium infiltration of the wood occurred only when those geological deposits were being emplaced at the time of the Flood several thousand years ago, instead of the 60 to 400 millions of years ago accepted by uniformitarian geology. I suggest at least part of the U-series disequilibria (19) found in the Colorado Plateau U deposits is because some U-daughter radionuclide separation occurred at the time of the Flood, and there has been insufficient time since then to reestablish equilibrium conditions.

The high U/Pb ratios and secondary ²¹⁰Po halos in the coalified wood samples from the Eocene epoch and the Triassic and Jurassic periods suggest to me that the wood in all these formations was in the same gel-like condition when infiltrated by the U-bearing solutions. To me these data represent evidence for a concurrent, single-stage invasion of U into all the different geological formations represented by the coalified wood samples. This is precisely what would be expected on the basis of a Flood-related phenomena.

The dual Po halos also fit well into the Flood scenario, i.e. the presence of a spherical and elliptical Po halo around the same radiocenter suggests a tectonic event occurred within 50 years after the initial infiltration of uranium into the wood samples. A readjustment of the earth's crust after such a massive event is not unexpected. Another implication of the existence of ²¹⁰Po halos in these specimens is that the transformation of the wood to a semi-coal-like condition must have occurred within a period of about one year. This evidence for a rapid coalification process is in contrast to the generally accepted view that coalification is a long-term geological process.

Three Types of Polonium Halos in Minerals

Now there are two other Po isotopes (²¹⁴Po and ²¹⁸Po) in the U decay chain besides ²¹⁰Po, but no halos representative of these other Po isotopes have been found in coalified wood. This is not surprising, because the half-lives of the other Po isotopes are rather short, i.e., t_½ = 3 m for ²¹⁸Po and t_½ = 164 μs for ²¹⁴Po as are the half-lives of the beta precursors of ²¹⁴Po, i.e. t_½ = 26.4 m for ²¹⁴Pb and t_½ = 19.8 m for ²¹⁴Bi (the precursor of ²¹⁸Po is the inert gas ²²²Rn). What is surprising is that all the three types of Po halos occur in certain minerals which typically contain orders of magnitude less uranium than the U-rich coalified wood. Further, the minerals such as biotite and fluorite must have diffusion rates considerably lower than those expected for a U-solution-infiltrated specimens of gel-like wood. Figure 7 shows the idealized structure of the different Po halos in comparison with the U halo.

Photographic evidence relating to the existence of different types of Po halos in minerals is shown in Fig. 1. Figure 1(n) shows three ²¹⁰Po halos of light, medium, and very dark coloration. The slightly higher radii for the darker halos is attributable to the higher dose. Figure 1(o) shows three different ²¹⁰Po halos in fluorite. Figure 1(p) shows a ²¹⁴Po halo in biotite, and Fig. 1(q) shows two ²¹⁸Po halos in biotite. Comparison of these halos with the idealized ring structure in Fig. 7 shows that Po halos in minerals can be clearly identified by ring structure studies alone. The data in Table 1 shows there is an excellent agreement between the experimentally produced He ion produced coloration bands and the Po halo ring radii.

An important observation from Fig. 7 is that in the idealized ²³⁸U and ²¹⁸Po patterns, it is evident that the ²²²Rn ring should be missing from the ²¹⁸Po halo and present in the ²³⁸U halo. Figures 8 and 9 show the presence of the ²²²Rn ring in the U halo in contrast to its absence in the ²¹⁸Po halo. This is unequivocal evidence that the ²¹⁸Po halo initiated with ²¹⁸Po rather than with any earlier alpha emitter in the U decay chain. Figures 10 and 11 show ²¹⁴Po halos and ²¹⁸Po halos in different types of biotite.

Henderson's (18) original idea that Po halos in minerals may have originated from a secondary source of radioactivity encounters formidable obstacles when closely examined. In most cases the minerals contain only ppm abundances of uranium, which means only a negligible supply of Po daughter atoms is available for capture at any given time. To form a halo these daughter atoms must migrate or diffuse so they can be captured at a collecting site, a problem which is compounded by the low diffusion rates in minerals (11,20,21). Despite these objections, in 1979 several investigators suggested their results (22) might provide support for secondary Po halo formation in minerals after all. They were apparently unaware that three years earlier I had reported the experimental observation of secondary ²¹⁰Po halos in coalified wood (17). In that report I discussed how even under the most favorable conditions (i.e., an abundant supply of U-daughters in a highly mobile environment) for the formation of secondary Po halos, only the longer half-life ²¹⁰Po halos actually formed, the reason being that the shorter half-life Po isotopes generally decayed away before they could be captured at the tiny Pb-Se sites. If these other two Po halo types didn't form under the best conditions in the gel-like wood, how could it be expected they would form naturally in the granites where diffusion rates are vastly lower and the supply of Po atoms is negligible?

The identity of U, Th and Po halos in minerals has been confirmed by analyzing the various types of halo radiocenters using scanning electron microscope x-ray fluorescence (SEMXRF) and ion microprobe mass spectrometric (IMMA) techniques (2,3). Studies of various Po halo radiocenters in biotite and fluorite have generally shown little or no U in conjunction with anomalously high ²⁰⁶Pb/²⁰⁷Pb and/or Pb/U ratios which would be expected from the decay of Po without the U precursor which normally occurs in U radiohalo centers (2,3). These results were obtained clearly in the analysis (3) of the most unusual array of Po halos which I ever found. That array, shown in Figure 12, has the appearance of a pair of spectacles, hence the designation 'Spectacle Halo.' The Spectacle Halo appearance compounds the problem of explaining its existence on the basis of known physical laws. In conclusion, in spite of attempts to define them out of existence (23), there is demonstrable evidence that Po halos do exist as separate entities (1-3).

Figure 7. Idealized schematic of 238U, 218Po, 214Po, and 210Po halos.

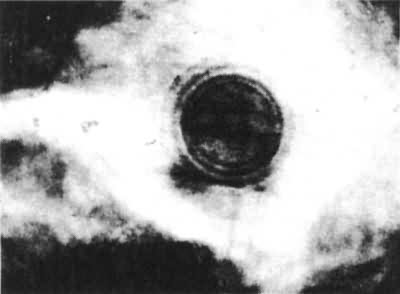
Figure 8. 238U halo in fluorite. (× 535)

Figure 9. 218Po halo in fluorite. (× 535)

Figure 10. 214Po halos in mica. (× 250)

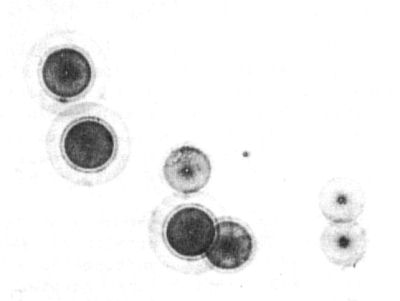
Figure 11. 218Po halos in mica. (× 250)

Figure 12. The Spectacle Halo, an overlapping series of 210Po halos discovered in a piece of biotite from the Silver Crater mine, Faraday Township, Ontario. Reproduced from ref. (3) by permission of Nature. (× 560)

Polonium Halos in Minerals: an Independent Evaluation

Because of the implications which will be attributed to the presence of Po halos in minerals, it is important that my colleagues be apprised of the independent investigation of these phenomena by Professor Norman Feather. In an exhaustive theoretical treatment (24) of the problem concerning their origin in minerals, Feather concludes it is difficult to account for the existence of Po halos in certain minerals on the basis of known physical principles. His exact words, as given in the synopsis of his paper, are as follows:

Ever since the discovery of Po-haloes in old mica (Henderson and Sparks 1939) the problem of their origin has remained essentially unsolved. Two suggestions have been made (Henderson 1939; Gentry et al. 1973), but neither carries immediate conviction. These suggestions are examined critically and in detail, and the difficulties attaching to the acceptance of either are identified. Because these two suggestions appear to exhaust the logical possibilities of explanation, it is tempting to admit that one of them must be basically correct, but whoever would make this admission must be fortified by credulity of a high order.

Polonium Halos and Primordial Rocks: a Test of the Hypothesis

I have advanced the hypothesis (25,26) that the three different types of Po halos in minerals represent the decay of primordial Po, in which case the rocks that host these halos, i.e., the Precambrian granites, must be primordial rocks (25,26). By this reasoning the Precambrian granites are identified as rocks that were created almost instantly as a part of the creation event recorded in Genesis 1:1 rather than rocks that are a product of the evolution of the earth. This rationale would be without scientific content if I had not also stated (25) that the laboratory synthesis of a hand-sized piece of granite or biotite would be accepted as falsifying my view that the Precambrian granites are created rocks and, likewise, that the subsequent production of ²¹⁸Po halos in that synthesized specimen of granite or biotite would be accepted as falsifying my view that Po halos in Precambrian granites originated with primordial polonium. The only response to my repeated (25,26) challenges to perform these laboratory syntheses and falsify the aforementioned evidences for creation has thus far been silence. It is inescapable that these experiments should be successful if the uniformitarian principle is true. Thus, with so much at stake for evolution, I suspect the reason why my evolutionary colleagues have failed to achieve success is because the Precambrian granites never formed by the uniformitarian principle to begin with; hence, to attempt to utilize it now to produce a synthesized piece of granite is just a futile effort. The end result is that the uniformitarian principle is essentially falsified because of its failure to live up to its own predictions. But since all the pieces in the evolutionary puzzle are glued together by this principle, we must now come to the same conclusion about evolution itself.

A Proposed Creation Model and the Age of the Earth

The evidence for creation cited above suggests there may have been special periods in earth history when physical laws as presently understood were insufficient to explain all the events transpiring within those periods. This evidence also undergirds the formulation of a creation model based on the Judeo-Christian ethic. The creation model proposed herein postulates that on at least three occasions (singularities) during the past 6000 years there were significant exceptions to the uniformitarian principle within our local cosmos (the Milky Way), viz., the ex nihilo creation of our galaxy about 6000 years ago, the Fall of man shortly thereafter, and the occurrence of a worldwide Flood about 4350 years ago. These ages are derived from Scriptural chronology. It is assumed that the creative act which brought the Milky Way into existence also caused the immediate propagation of light throughout the galaxy. No constraints are placed on the age of the universe.

Singularities and Uniformities: A Complementary Approach

It is essential to understand that uniform action of physical laws between singularities is an integral part of this creation model. Moreover, the occurrence of a singularity does not mean a completely chaotic condition without any laws to govern the operations of nature during that period. During the Flood singularity some physical processes may not have changed at all whereas there is evidence others varied considerably. An enhanced radioactive decay rate during the Flood singularity would have generated a considerable amount of heat, thus initiating volcanic and tectonic activity during and after that period. This three-singularity model appears to be the minimum framework that includes the essential features of the Genesis narrative. Possibly the continent-separating episode recorded in Genesis 10:25, when the earth was divided in the days of Peleg a few hundred years after the Flood, should also be included as a singularity; certainly it must figure prominently in any creation-based reconstruction of earth history that deals with continental drift. However, to simplify matters, the following comments exclude consideration of this event.

Singularities and the Interpretation of Radioactive Decay as Elapsed Time

In summary, the creation model envisions an initial creation singularity followed by a short period of uniformity until the second singularity, an event which involved degenerative changes in the biological world and quite possibly modification of some of the original physical laws which governed the earth and our near celestial environment. Another period of uniformity follows, with the modified physical laws now in effect, for about 1600 years down to the longer-duration Flood singularity. The last period of uniformity extends down to the present. In this scenario U/Pb ratios are presently utilized as indicators of elapsed time since the last singularity. ²³⁸U/²⁰⁶Pb ratios are not used as time measures prior to this last singularity because of conflicting evidence of very high Pb and He retention in natural zircons subjected to a prolonged high temperature environment in deep granite. Those results, discussed below, are consistent with a very young age of the earth, and suggest that the radioactive decay rate may have been enhanced (indeed, had to be if this creation model is correct) during any one of the three singularities. (The Peleg episode potentially adds one more possibility.) The assumption of uniform decay since the Flood is the basis for interpreting the very high U/Pb ratios in coalified wood samples as evidence for a several-thousand-year age of specimens which conventional geology holds to be about 60 to 400 million years old.

Possible Evidence of Enhanced Radioactive Decay from 'Blasting' Halos

Additional evidence for an enhanced radioactive decay rate comes from Ramdohr's observations on fractured radioactive halos in polished ore sections. He reports (27) that certain radioactive inclusions, which exhibit a considerable volume increase due to isotropization from radioactive decay, have in numerous cases been observed to fracture the surrounding mineral in a random pattern. Ramdohr points out that the surrounding mineral should expand slowly over geological time due to radioactive isotropization, and individual cracks should appear as soon as the elastic limit is reached. He further points out that, while these expansion cracks should occur first along cohesion minimums and grain boundaries, nothing like this happens. Individual cracks surrounding the radioactive inclusion are randomly distributed and evidently occur quite suddenly in the form of an explosive fracture and not a slow expansion. Ramdohr shows many photographs of instances wherein the central inclusion fractures the non-isotropic outer zone. The occurrence of this phenomenon is worldwide.

While there might be other alternatives, one possible explanation of these "fractures" or "blasting" halos is that the rate of radioactive decay was at one time far greater than that observed today. The isotropization of the host minerals would have occurred very rapidly due to an anomalous decay rate, and hence fracturing of the outer mineral would be expected.

The Age of the Earth and Pb Retention in Deep Granite Cores

Results pertaining more specifically to a recent creation of the earth come from studies of Pb retention in zircons taken from deep Precambrian granite cores (28). To understand the rationale for this last statement, it must first be understood that the Pb in these zircons is primarily a secondary trace component derived from the decay of small amounts of U and Th. Secondly, this radiogenic Pb has a tendency to migrate or diffuse out of the zircon crystals far more rapidly than the parent U and Th because these elements are relatively tightly bound in lattice sites, whereas the Pb atoms really do not fit into the zircon lattice. Further, since all elements show an exponential increase in the bulk diffusion rate with increasing temperature, and since the temperature in the granite cores increases significantly from near the top (105°C) to the bottom (313°C) of the granite portion of the drill hole, calculations show that 50 μm-size zircons taken from the bottom of the drill hole (313°C) should have lost 1% of their Pb content in about 300,000 years. Since the zircons were in cores taken from a Precambrian granite that is estimated to be 1.5 billion years old by conventional geochronology (29), the prediction based on uniformitarian geochronology would be that most of the Pb would have long ago diffused out of the zircons extracted from the deepest cores at 313°C. But the results of the experiments did not agree with this prediction; rather they showed equally high retention of Pb in zircons taken from all depths. In fact no Pb loss from zircons at 313°C would appear to place an upper limit to the age of this Precambrian granite, which, on the presumption that these granites are primordial rocks, in essence places the same limit on the age of the earth.

The Age of the Earth: Limited by Helium Retention in Deep Granite Cores

Another approach which seemed to hold greater prospects for more closely defining an upper limit for the age of these Precambrian granites (and hence of the earth) was the differential analysis of similar size zircons from these same cores for helium, the second most volatile chemical element known. The helium accumulates in these zircons in a manner similar to the radiogenic Pb, viz., from the alpha particles emitted from trace amounts of U and Th. However, the extreme volatility of this gas means that it diffuses out of the zircons at a far greater rate than Pb. On a purely uniformitarian basis the search for helium in these zircons would quite possibly never have been done because conventional geological wisdom suggests negligible helium retention in zircons subjected to even 100°C for the presumed 1.5 billion year age (29) of those granites. But having already discovered that the Pb retention in these zircons contradicted the age estimates determined by radiometric dating techniques, I decided that, from a creationist perspective, the search might just reveal something of exceptional interest. Groups of zircons from six different depths were repeatedly analyzed for helium using an extremely sensitive gas mass spectrometric system. The results (30) showed a helium retention of about 58% in the tiny 50 μm zircons from 960 meters depth (105°C), about 27% in zircons from 2170 meters (151°C) and a phenomenal 17% retention of helium even at 2900 meters where the temperature is 197° C. These results show a creation-based perspective of science does possess predictive capabilities which can be scientifically tested.

It is difficult to understand how such high retention (30) of helium can be accounted for except by restricting the age of these granites (and hence the earth) to something of the order of several thousand years. These results are consistent with an approximate 6000-year age of the earth and moreover are in direct conflict with the presumed 4.5-billion-year age of the earth determined by radioactive dating techniques. Evolutionary colleagues can prove this deduction for a young age of the earth is wrong if they can show just how this unusually high retention of helium can be deduced from the accepted 1.5-billion-year age (29) of those zircons by using only uniformitarian principles.

A Creation Model of the Structure of the Universe

Decades of research in astronomy and cosmology have led to the general belief that the present state of the universe can ultimately be traced to an initial event popularly known as the Big Bang. Despite this popularity it should be remembered that the Big Bang cosmological model is only as valid as the fundamental premises which support it. Thus the discussion of the proposed creation model of the universe must necessarily also focus on the validity of the Big Bang theory, whose basic framework consists of the cosmological and uniformitarian principles together with the general theory of relativity. The previous sections of this article have documented the failure of the uniformitarian principle to provide confirmation for the geological evolution of the Precambrian granites. If this principle cannot account for the evolution of the earth, is it difficult to understand how it can provide a rational basis for constructing an evolutionary model of the universe. It may be argued, however, that the edifice of modern cosmology fits together too well for there to be something wrong with basic assumptions. This point will receive close examination in the following discussion of the hot Big Bang Model (31,32).

The Big Bang Model and the Hubble Relation

About 50 years ago Hubble proposed that the astronomical data then available seemed to linearly relate the redshift z of a galaxy with the distance R to the galaxy, and this has become known as the Hubble relation. Since then galactic redshifts have been mainly interpreted as Doppler shifts resulting from high recessional velocities of the distant galaxies and, moreover, have been generally thought to provide some of the strongest evidence for the hot Big Bang model of an expanding universe. (See, however, Hetherington's evaluation (33) of the Hubble relation.) The reason for confidence in this interpretation is that by using the general theory of relativity as the mathematical basis for calculating the space-time development of the primeval fireball, it is possible to derive the z ∝R Hubble relation (31,32) provided certain assumptions are made.

Notwithstanding the general belief that the accumulated astronomical data do support a z ∝ R relation, the fact is that over the past two decades several detailed studies of redshift distributions have been published which call the Hubble relation into question. As early as 1962 Hawkins (34) claimed that the redshift data indicated an approximate quadratic-distance redshift relation, in particular z ∝ R^2.22. More recently the case for a z ∝ R² relation (for low z) was considerably reinforced by the extensive statistical analyses of Segal (35) and of Nicoll and Segal (36). Even though these latter results have been disputed by Sandage et al. (37), it appears that Nicoll and Segal (38) have responded with stronger evidence for a z ∝ R² relation. In fact, Nicoll et al. (39) have gone so far as to claim statistical invalidation of the Hubble relation for low values of z. At a minimum the foregoing results make it very difficult to believe that the redshift data as presently interpreted actually support the Hubble relation, which is the cornerstone of Big Bang cosmology.

As noted above, the latest analyses of Nicoll and Segal (38) show the redshift data more closely fit what is thought to be the equivalent of a quadratic rather than a linear distance relation. The reason for qualifying the last statement is because astronomers measure not distances but apparent magnitudes, which are first corrected for various factors before being used as a basis for establishing the magnitude-redshift relation. One important correction involves the assumption that the galactic light intensity (for any given frequency interval) as observed on earth is reduced by two factors of 1 + z, one for the redshift itself, and the other for the presumed galactic recession. Of course if the galaxies are not receding, then an unwarranted factor has been introduced into the magnitude correction procedures, and this would affect the perceived redshift distributions.

The Big Bang Model and the Cosmic Microwave Radiation (CMR)

In 1978 Penzias and Wilson received the Nobel prize in physics for their discovery of the CMR in 1965. Since then it has been widely claimed that this pervasive radiation field is a relic of the time eons ago when radiation quanta decoupled from matter in the primeval fireball (31). According to this theory, the decoupling presumably occurred about 300,000 years after the Big Bang when the primeval fireball had expanded and its temperature had dropped to the point where matter and radiation ceased to interact as it had before. After this time, supposedly about 15 billion years ago, it is believed that this radiation propagated throughout space in an unobstructed fashion to eventually become the CMR. It is essential to note that the radiation leaving the primeval fireball at the time of decoupling was presumably still quite hot (about 3000°K). The experimental measurements of the CMR temperature at present reveal that it is very cold (3°K). But if the radiation from the primeval fireball is assumed not to interact with matter after the time of decoupling, then how did this initially hot radiation lose its energy, or temperature, to later become the 3°K CMR? The standard explanation is that the general relativistic analysis of the space-time expansion of the primeval fireball predicts that the decoupled radiation quanta will lose energy just as a result of the expansion of the universe. There is, however, nothing in modern experimental physics which suggests that radiation quanta change energy by moving through free space. Thus, the standard explanation for this remarkable thousand-fold energy loss in the decoupled radiation quanta depends upon an aspect of general relativity that is unsupported by scientific evidence.

To avoid possible misunderstandings, some recent experimental results of gravitational effects on photons will be discussed. Einstein's principle of equivalence, which is independent of general relativity, does not distinguish whether a photon traversing a gravitational potential gradient undergoes a change in energy in transit, or whether its energy is uniquely determined by the gravitational potential at the point of emission. The earliest Mossbauer experiments (40) on the gravitational redshift could not distinguish between these two alternatives, and it was widely believed that the photon energy could change when passing through a difference in gravitational potential. But recent experimental results (41) suggest the photon energy is characterized by the gravitational potential at the point of emission rather than varying as the photon moves to a different potential. In the light of these results it is quite difficult for me to believe that radiation quanta can undergo energy loss in free space as predicted in the general relativistic Big Bang model. At this point my views on the theory of relativity need to be clarified.

I recognize there are some notable experimental results in physics such as apparent time dilation, the transverse Doppler effect, the increase in mass with velocity, and the gravitational bending of light, which are in accord with the predictions of the theory of relativity. However, these experimental results cannot be used as confirmations of the special or general theory of relativity because there are other (albeit far lesser known) theories which predict similar results. (See for instance North's (42) review of various alternative theories of gravitation and their predictions.) Further, recently Rastall (43) and especially Marinov (44) have shown independently that it is not necessary to assume the general relativistic framework to obtain many of the same mathematical results. On the other hand, the question of whether the Big Bang model is a correct description of the origin and evolutionary development of the universe is entirely hinged on the ultimate validity of general relativity's fundamental postulate, which in principle denies that privileged reference frames exist. Very germane to this discussion is the recent admission (45) of an eminent physicist to the effect that the CMR presents undeniable experimental evidence for the existence of an absolute reference frame in the universe, a result which is consistent with Marinov's (44) evidence for absolute space-time and also with at least one of the earlier gravitational theories reviewed by North (42). This point is treated in more detail subsequently and it is shown that the existence of the CMR as an absolute reference frame is perhaps the most important evidence that can be adduced for the creation model of the universe as proposed herein. Before engaging in this discussion further, it is necessary to complete the present discussion of the CMR and the Cosmological Principle.

Measurements have shown the spatial distribution of the CMR is so uniform that it is questionable whether it could have been produced by the Big Bang scenario as it was originally conceived. Weisskopf (45) has recently reviewed the nature of this and other problems with the Big Bang model, and has discussed the provisional solutions offered by postulating an explosive expansion in the very early stages of the Big Bang. Questions still remain, however, not the least being that the entire scenario assumes some type of grand unification theory which has yet to be verified. But is it consistent for cosmologists on one hand to claim that the universe evolved only through the action of known physical laws and on the other hand to devise solutions to cosmological problems by using unverified hypotheses as a basis for those solutions? We have already noted the failure of the uniformitarian principle to successfully account for the origin of Po halos in Precambrian granites, or to provide a basis for synthesis of a piece of granite. In a similar manner it seems the introduction of unverified physical concepts as the basis for possible solutions to difficult evolutionary cosmological problems is just the inevitable result of the failure to explain the creation of the universe on the basis of the uniformitarian principle. In any event, the newly proposed expansionary modification to the Big Bang only deals with the earliest instants of the Big Bang, after which it is supposed the expansion of the primeval fireball continues as envisioned in the original Big Bang model. As we shall soon see, it appears there may be a contradiction involved in the theoretical development of expansion of the fireball.

The Big Bang Model and the Cosmological Principle

In spite of the foregoing difficulties it might still be argued that Big Bang model must be correct because it predicts a universe in accord with the Cosmological Principle, viz., that the universe appears the same irrespective of the location of the observer in the universe. The problem with this argument is that we really do not know the Cosmological Principle is true. In fact, all that we know is that the large scale structure of the universe appears to be approximately isotropic (i.e., the same in all directions) from our present point of observation. Modern cosmology justifies the Cosmological Principle by coupling the observation of isotropy about our position with the assumption that our galaxy does not occupy a special position in the universe. That is, if our galaxy occupies a non-specific or arbitrary position in the universe, then it follows the universe must be isotropic everywhere and hence homogeneous as well.

But what if our galaxy does occupy a privileged position in the universe? First, it would no longer be logical to extrapolate the isotropy which we observe to the other parts of the universe, which means it would no longer be possible to justify either the condition of homogeneity or the cosmological principle. Second, the simplest deduction of the observed isotropy of the universe from our location is that the universe must be spherically symmetric about either the Milky Way or some point which is astronomically nearby. But spherical symmetry about any point in the universe implies that point is the Center, and this brings us to the discussion of the creation model.

A Creation Model of the Universe: The Fundamental Postulate

The fundamental premise of the Judeo-Christian creation model of the universe is determined by the scripture, "The Lord has established His throne in the heavens, and His kingdom ruleth over all." Psalm 103:19 (RSV). On the basis of this statement it is evident that the Creator has established, or fixed, His throne at some point in the universe, which in my view is none other than the Center of the universe. It is axiomatic that a fixed point in the universe requires the existence of a fixed or absolute reference frame. Previously it was noted that the CMR has been recognized as establishing an absolute reference frame (45); so it is quite clear that the fundamental postulate of this creation model of the universe is based on tangible scientific evidence.

The Revolving Steady State Model of the Universe: A Brief Description

Assuming there is a Center (C) to the universe, I propose that the galaxies are not receding from each other as presently supposed, but instead are revolving at different distances and at different tangential speeds around C. On this basis all galaxies must have a tangential velocity around C. Measurements have shown that our solar system, and hence the Milky Way, has a cosmic velocity through the CMR (46), and it is this velocity which is identified with the tangential velocity of the Milky Way around C. In this view C must lie somewhere in that plane which passes through the MW which is also perpendicular to the cosmic velocity vector of the MW. It is evident that the RSS model pictures the galaxies orbiting C in any one of many different-sized concentric shells which suggests the alternate designation 'Shell Model of the Universe.'

As originally conceived this Revolving Steady State (RSS) model envisions a universe with galaxies which move in circular orbits under the gravitational field produced by all of them. The field is assumed to be stationary and spherically symmetric. Decades ago Einstein made a general relativity study (47) of circulating particles constrained by this type of gravitational field, but his analysis did not mention redshifts, nor was there any hint that he considered his analysis had any reference to the structure of the universe.

The RSS Model and Galactic Redshifts

Assuming the galaxies are revolving in different orbital planes and with different tangential velocities v around some universal center C, initially I thought that if the Milky Way was one of the innermost galaxies, then most of the galactic redshifts as observed on earth might be due to a combination of gravitational and transverse Doppler effects. (A literature search showed that Burcev (48) had proposed over a decade ago that quasars were possibly stellar objects whose redshifts might be attributable to the transverse Doppler effect.)

Although questions have arisen about this explanation for the galactic redshifts in the RSS model, it seems worthwhile to explain my original rationale and the objections which now appear to present themselves. In particular, in the Newtonian-based RSS model the galaxies of mass m and tangential velocity v remain in circular orbits by gravitational attraction of the total mass M within the sphere of orbital radius R. In this scenario, mv²/R = mMG/R², or v² = GM/R, where G is the gravitational constant. Thus an observer on an innermost galaxy located at a distance R₁ from C would in theory see light from a more distant galaxy (at R₂ from C) shifted in frequency because of the transverse Doppler effect and the change in gravitational potential V(R) = −GM/R. The presumed limiting distance R' at which galaxies could remain in stable orbits would be when the tangential velocity v = c, the velocity of light. Beyond this presumed galactic cutoff distance the RSS model tentatively assumes a rapidly diminishing mass/energy density so that we do not encounter an infinite gravitational potential (see discussion of equations (2) and (3) for more details).

The frequency shifts expected in the RSS model can be compared to an earth-bound observer comparing the frequency of a light signal emitted from his position on the rotating earth's surface, where the tangential velocity is v₁, and the gravitational is V₁, with the frequency of the same signal emitted from an overhead satellite which is orbiting with velocity v₂ in a gravitational potential V₂. The experimentally confirmed (41) equation for the redshift, as derived from the principle of equivalence, is:

(1)	z = (V1 − V2) / c2 − (v12 − v22) / 2c2.

The same equation applies in the RSS model except that v₁ and V₁ are the cosmic velocity and gravitational potential of the Milky Way at R₁ from C whereas v₂ and V₂ represent the same quantities for a more distant galaxy at R₂ from C.

Another source of frequency shifts arises because the Milky Way (MW) is not exactly at C. In this case the more distant galaxies, which are rotating away from or toward the MW, produce first order Doppler redshifts or blueshifts. The blueshifts, which would be most pronounced for nearby galaxies, can be eliminated for all practical purposes if it is assumed that the more distant galaxies are rotating away from the MW. This scenario would result in a recessional redshift which, because it depends on the cosine of the angle between the velocity vector of the outer galaxy and the line of sight from the MW to that galaxy, would diminish with distance. Thus, of itself this redshift could at most be only a part of the total galactic redshift observed on the earth. Of course, a significant distance-related redshift, irrespective of its origin, could overshadow most blueshifts expected from galaxies rotating toward the MW and eliminate the need for assuming rotation away from the MW.

We now return to the discussion of the redshifts expected on the basis of eq. (1). If the ρ, the mass/energy density of the universe is assumed to be constant then M = 4 πρ R³/3, and substitution of the appropriate quantities into eq. (1) leads to the formal result that z is proportional to R², which is of the same form of the redshift relation proposed in references (33,34,37-39). On a similar basis, if the density is assumed to vary inversely as R, then one can obtain an expression for z which is proportional to R, which is of the same form as the Hubble relation (49).

Of course, astronomers measure apparent magnitudes, not distances, and, for there to be a quantitative comparison between the above results and the redshift distribution, the light flux relation for the RSS model must be formulated so as to include the combined effect of the redshift and gravitational focusing. This formulation has yet to be done; thus on this basis alone it would be premature to claim the forgoing results are consistent with the galactic redshift relation proposed by Nicoll and Segal (38). Moreover it should be remembered that if the universe is revolving, then an extraneous factor has been included into the data which comprise the redshift distribution, and this would preclude any immediate comparison. But regardless of the outcome of the above calculations, there seems to be a more fundamental objection to the preceding formulation.

In particular, we must carefully investigate whether the gravitational potential V = −GM/R used in the above calculations is the correct expression for the potential function. It is of crucial importance to know whether it is correct for it is used as the basis for the derivation of the Hubble relation (31,32) in Big Bang cosmology. According to Silk (31) and Weinberg (32), its use in computing the potential at the surface of an arbitrarily large, but finite sphere, of radius R within an infinite universe is justified by a theorem due to Birkhoff. Part of the proof of this theorem implicitly assumes that the universe is structured according to the Cosmological Principle. Now the creation model of the universe proposed herein is also of infinite extent, but the Cosmological Principle does not hold, so that there is no basic reason why this theorem should yield the correct gravitational potential in the RSS model. But should it hold for the Big Bang model?

To answer this question we first note that the negative gradient of the potential V = −GM/R yields a repulsive force per unit mass F/m = GM/R² whereas there is an experimentally confirmed theorem in classical mechanics which definitely requires an attractive force per unit mass F/m = −GM/R² to exist at any point R within a sphere enclosing a uniform mass distribution. This latter result is an integral part of both the RSS and the Big Bang models. Thus the potential V = −GM/R is just as wrong for the Big Bang model as it would be for the RSS model because it yields an incorrect sign for the force. Even Silk's (31) elementary treatment (see page 332) makes it clear that the derivation of the Friedmann equation for the Big Bang expanding universe is based on the potential V = −GM/R. Here we have a logical contradiction in the theoretical development of the primeval fireball, which is of course the basis for predicting the Hubble relation in the Big Bang.

An expression for the potential (50,51) which does yield the correct attractive force is given by

(2)	V(R) = −GM/R     − G ∫R∞ 4 πρ r dr     where M = 4π ∫oR ρr2dr.

The problem here is that for a finite, uniform density we encounter an infinite potential due to the presumed infinite size of the universe. This result is the same for both the Big Bang model and the RSS model.

Alternatively, a finite potential can be obtained from eq. (2) by assuming the density diminishes more rapidly than 1/R³ after R', where v = c. As a first approximation this assumption truncates the potential at R'. In this case the upper integration limits in eq. (2) must be changed from infinity to R', and we have the following potential:

(3)	V(R) = −GM/R     − G ∫RR' 4 πρ r dr     where M is defined in eq. (2).

If this potential is used in eq. (1) to compute z for the RSS model, then for a uniform density for all R less than R', we find the redshift is zero. If, however, the density increases as R^0.22 then we can formally obtain a relation (51) similar to that deduced by Hawkins (34). Again, however, it is premature to make any claims about this result until more work is done.

Another possibility for obtaining redshifts in the RSS model is to assume the mass/energy density diminishes as 1/R⁴. In this case the galactic orbits are no longer circular but spirals, and there is a recessional component to the velocity which leads to a first order Doppler shift and a Hubble type z ∝ R relation. For this view to have any credibility most of the mass/energy of the universe must be in a form other than the matter and radiation energy presently observed and/or inferred in stellar systems and intergalactic dust. In this context it is perhaps worth mentioning that Ellis (52) has proposed that there may be a large amount of undetected mass/energy in other forms (e.g., neutrinos) which could raise the cosmic mass/energy density to more than a million times the present density estimates of 10⁻³¹to 10⁻²⁹g/cm³.

Of course the RSS model does not require that the redshifts are velocity dependent. In this respect it is well known that years ago proponents of a static or steady state universe proposed a variety of distance-dependent interpretations of the redshift which were non-recessional in nature (see North's (42) review for details and references). The investigation of the origin of the redshifts in the RSS model should include a reexamination of these alternatives.

Estimates of the Distance from the Milky Way to the Center

Earlier it was implied that the Milky Way could be one of the innermost galaxies in the RSS model. This view is based on the assumption that the Milky Way's cosmic galactic velocity of 550 km/s through the CMR (46) is just the tangential velocity of the Milky Way (MW) around C. Galactic peculiar motions may also be of the same nature. On this basis we can compute the angular velocity ω of the MW around C from v² = ω²R² = GM/R, which leads to the result that ω = 2(πρG/3)^½.

For a constant ρ = 10⁻²⁹g/cm³, then ω = 5 × 10⁻¹¹ rad/y, and the distance from C to our galaxy would be about 3.7 × 10⁷ light-years. (C of course would be located somewhere in the plane perpendicular to the direction of the motion of the MW through the CMR.) If ρ = 10⁻²⁷g/cm³ then ω = 5 × 10⁻¹⁰ rad/y (or 5 × 10⁻⁵ arc-s/y), which means that differential angular motions of the more distant galaxies (as observed at the MW) would still be below the present detection limit of light telescopes (≃10⁻³ arc-s/y). In the latter case the distance from the MW to C is about 3.7 × lO⁶ light-years and is considered the preferred value so as reduce potential blueshift effects. This distance places C outside our galaxy but still in the plane which is perpendicular to the MW's cosmic velocity vector. No observational data as yet seems to locate the direction of C in that plane. On the other hand Orion is in that plane, and is prominently mentioned in Scripture (Job 9:9; 38:31; Amos 5:8). As a working hypothesis I suggest that C may lie a few million light years beyond Orion. One density used in the preceding calculations is higher than current estimates but, as previously noted, Ellis (52) has suggested there may be a large amount of undetected mass/energy which may raise the value to more than 10⁻²⁴ g/cm³. On this basis the higher density estimate is not unreasonable. In the RSS model the value of the density cannot much exceed 10⁻²⁶ g/cm³ or else the angular velocity will increase to the point where differential motions of distant galaxies would be observed.

The RSS Model and Olber's Paradox

We briefly digress to note that Olber's Paradox is resolved if the universe is structured according to the RSS model because the finite number of galaxies within a sphere of radius R' will only produce a finite light flux at the Milky Way. Even if there is luminous matter beyond R', the density is assumed to diminish so rapidly that the light flux received at the Milky Way from beyond R' will also be finite.

The RSS Model and Varshni's Analysis of Quasar Redshifts

In the context of the present proposal for the structure of the universe it is most appropriate to refer to Varshni's (53) investigation of the redshift distribution of 384 quasars. From a probability analysis of those 384 quasars he found an astounding 57 sets of redshift coincidences within small redshift intervals. Varshni calculates the probability of chance coincidence of these groups to be about 10⁻⁸⁵. He concludes that if quasar redshifts are real (he thinks they are not) and are of cosmological origin (i.e., distance related), then the only logical deduction from the data is, in his own words, as follows:

The Earth is indeed the center of the Universe. The arrangement of quasars on certain spherical shells is only with respect to the Earth. These shells would disappear if viewed from another galaxy or a quasar. This means that the cosmological principle will have to go. Also, it implies that a coordinate system fixed to the Earth will be a preferred frame of reference in the Universe. Consequently, both the Special and the General Theory of Relativity must be abandoned for cosmological purposes.

These deductions are amazingly similar to the deductions of the RSS model except that, first, the earth, or MW, is only astronomically close to rather than being exactly at the Center, and, second, the absolute reference frame is defined by the CMR and not the position of the earth. And from earlier discussions in this article, it should now be clear that the special and the general theory of relativity are not credible theories in the RSS model. In fact, as shown below, if anything it now appears that the results of one of the most celebrated experiments in the history of physics contradict the basic premises of both special and general relativity so directly that, to me at least, it seems these theories are no longer tenable. As noted earlier, however, just because special and general relativity are shown to be untenable does not invalidate all the mathematical results obtained by these theories. It suggests rather that there must exist an absolute space-time framework which would encompass all the results of relativity which do accord with experiment, but different results where relativity theory makes incorrect predictions. Several investigations pertaining to this alternative framework have already been cited (42-44). In addition we should also mention Clube's (54) work and his exchanges with others (55) on neo-Lorentzian relativity.

The RSS Model, the CMR, and the Theory of Relativity

Clube's (54) explanation for the CMR is undergirded by the assumption of a non-relativistic Lorentz invariant material vacuum. It is intriguing to consider that the CMR may be the result of emissions from a cold material vacuum. On a related matter, Clube cites other work (56) as evidence that observations are not at all inconsistent with an essentially Euclidean infinite cosmos. Certainly these ideas appear easily reconcilable with the RSS model since they assume the existence of an absolute reference frame. However, the details of Clube's theory have yet to be worked out so it is premature to make any claims until further work is done. Of course there is also the possibility that the CMR may be a part of the 'light' that was created in Gen. 1:3. Interestingly, Weisskopf (45) alludes to that very possibility in the closing paragraph of his recent article:

Indeed, the Judeo-Christian tradition describes the beginning of the world in a way that is surprisingly similar to the scientific model. Previously, it seemed scientifically unsound to have light created before the sun. The present scientific view does indeed assume the early universe to be filled with various kinds of radiation long before the sun was created. The Bible says about the beginning: "And God said, 'Let there be light'; and there was light. And God saw the light, that it was good."

Irrespective of how it originated, the most important fact about the CMR is that it represents unequivocal evidence of an absolute reference frame in the universe, a very necessary condition in the RSS model, but an inconsistent condition for the relativistic foundations of the Big Bang model. To explicitly show exactly how this inconsistency arises, it is most helpful to include another quote from Weisskopf's recent article:

It is remarkable that we now are justified in talking about an absolute motion, and that we can measure it. The great dream of Michelson and Morley is realized. They wanted to measure the absolute motion of the earth by measuring the velocity of light in different directions. According to Einstein, however, this velocity is always the same. But the 3K radiation represents a fixed system of coordinates. It makes sense to say that an observer is at rest in an absolute sense when the 3K radiation appears to have the same frequencies in all directions. Nature has provided an absolute frame of reference. The deeper significance of this concept is not yet clear.

With all due respect to my eminent colleague I suggest the meaning of this fact is not obscure at all. I suggest the evidence (the CMR) which has received worldwide acclaim as confirmation of the Big Bang is in reality its death knell for, ironically, it is now clear that the existence of the CMR essentially falsifies the fundamental postulates of the theory of relativity. The logic is quite straightforward. Referring to the last quotation by Weisskopf, we note he mentions the famed Michelson-Morley experiment, which achieved only a null result.

Lorentz's efforts to explain this null result on the basis of an absolute reference frame were supposedly untenable. The real explanation, according to almost every physics textbook written in the past 60 years, was given by the theory of relativity, namely that: Given the null result of the Michelson-Morley experiment, if the fundamental principles of relativity are true, then there is no absolute reference frame. But the CMR is an absolute reference frame, so the original relativistic deductions about the Michelson-Morley experiment are in error. More precisely, since logic requires the contrapositive of a statement to be equivalent to the statement itself, the preceding "if relativity is true, then no absolute reference frame" statement must be equivalent to "if an absolute reference frame exists, then the fundamental principles of relativity are untrue." In simpler terms the theory of relativity has been falsified because a major prediction of the theory is now known to be contradicted by an unambiguous experimental result. Without relativity theory there is no Big Bang, no Hubble relation for the redshift, and no explanation for the CMR in an evolutionary cosmological model.

Acknowledgments, Reflections, and Conclusions

Special thanks goes to Drs. Frank Awbrey and Bill Thwaites, Biology Department, San Diego State University, for extending to me the opportunity of participating in this symposium, and for their understanding and patience during the revision of this contribution. Special thanks also to Dr. Alan Leviton, Director, Pacific Division of the AAAS, who very kindly undertook the task of translating my computer disks into a finished manuscript.

Several years ago the American Physical Society sent its members a copy of the National Academy of Sciences resolution of April 1976, "An Affirmation of Freedom of Inquiry and Expression," which reads in part ". . . That the search for knowledge and understanding of the physical universe and of the living things that inhabit it should be conducted under conditions of intellectual freedom, without religious political or ideological restrictions. . . . That freedom of inquiry and dissemination of ideas require that those so engaged be free to search where their inquiry leads . . . without political censorship and without fear of retribution in consequence of unpopularity of their conclusions. Those who challenge existing theory must be protected from retaliatory reactions."

In recent years the lofty aim of that resolution has not been realized as I have tried to pursue my research. In my opinion some of my more influential colleagues have found it easier to support this NAS resolution for foreign dissident scientists than for an American scientist who dissents from evolution. In fact I read in a recent issue of Science (57) that the NAS itself has recently stepped up its anti-creation campaign by the widespread distribution of a publication which claims that creationism is not science. I will present the opposite viewpoint in my forthcoming book (58) while also relating some details concerning my difficulties in pursuing research in this somewhat controversial field. The impact of aforementioned NAS resolution on my research efforts receives special attention.

In closing I wish to express my gratitude to those of my evolutionary colleagues who on so many occasions have assisted me, and on other occasions have collaborated with me in my research. Of one thing I am certain: Only in America could my research over the past two decades have been accomplished. I close by expressing gratitude to my Creator for allowing me the privilege of being an American. I submit this article to the scientific community not as an antagonist who purports to have the last word on the subject, but as a colleague who, in the spirit of free scientific inquiry, genuinely seeks a vigorous, critical response to the evidence presented herein. Perhaps a future "Evolutionists Confront Creationists" AAAS symposium would be the ideal forum for this exchange to occur.

References

1. Gentry, Robert V. 1973. Annual Rev. Nucl. Sci. 23: 347.
2. Gentry, Robert V. 1974. Science 184: 62.
3. Gentry, Robert V. et al. 1974. Nature 252: 564.
4. Joly, J. 1917. Phil. Trans. Roy. Soc. London Ser. A. 217: 51-79; Idem. 1917. Nature 99: 457-58, 476-78; Idem. 1923. Proc. Roy. Soc. London Ser. A 102: 682-705; Idem. 1924. Nature 114: 160-64.
5. Kerr-Lawson, D. E. 1928. Univ. Toronto Stud. Geol. Ser. No. 27:15
6. Henderson, G. H., C. M. Mushkat, D. P. Crawford. 1934. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 158: 199.
7. Henderson, G. H., and L. G. Turnbull. 1934. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 145: 582.
8. Henderson, G. H., and S. Bateson. Ibid., Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 145: 573.
9. Schilling, A., 1926. Neues Jahrb. Mineral. Abh. 53A: 241. See also Oak Ridge Nat. Lab. Rep. ORNL-tr-697.
10. Mahadevan, C., 1927. Indian J. Phys. 1: 445.
11. Gentry, Robert V. 1968. Science 160: 1228.
12. Gentry, Robert V. 1971. Science 173: 727.
13. Gentry, Robert V. et al. 1973. Nature 244: 282.
14. Gentry, Robert V. 1978. Are Any Unusual Radiohalos Evidence for SHE? In Proc. International Symposium on Superheavy Elements. Lubbock, March 1978. Pergamon Press, New York, Oxford.
15. Gentry, R. V., W. H. Christie, D. H. Smith, J. W. Boyle, S. S. Cristy, & J. F. McLaughlin. 1978. Nature 274: 457.
16. Gentry, R. V. 1970. Science 169: 670.
17. Gentry, R. V., W. H. Christie, D. H. Smith, J. E. Emery, S. A. Reynolds, R. W. Walker, S. S. Cristy, & P. A. Gentry. 1976. Science 194: 315.
18. Henderson, G. H. and F. W. Sparks 1939. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 173: 238. Henderson, G. H., ibid., p. 250.
19. Lind, S. C., and C. P. Whittemore. 1915. U.S. Bur. Mines Tech. Pap. 88:1. Stern, T. W., and L. R. Stieff, 1959. U.S. Geol. Surv. Prof. Pap. 320:151. Rosholt, J. N., 1958. In Proceedings of the Second U.N. International Conference on the Peaceful Uses of Atomic Energy, Geneva. United Nations, New York, vol. 2, p. 321.
20. Gentry, Robert V. 1975. Nature 258: 269.
21. Fremlin, J. H. 1975. Nature 258: 269.
22. Hashemi-Nezhad, S. R., et al., 1979. Nature: 178: 333-335.
23. Moazed, C., R. M. Spector, and R. F. Ward. 1973. Science 180: 1272.
24. Feather, N. 1978. Roy. Soc. Edinburgh Commun. 11: 147.
25. Gentry, Robert V. 1979. EOS 60: 474. Idem. 1980. EOS 61: 514.
26. Gentry, Robert V. 1982. Physics Today 35: No. 10, 13. Ibid., 36: No. 4, 13.
27. Ramdohr. P. 1957. Abb. der Deutsch. Adad. d. Wiss., Berlin, Kl. f. Chem., Geol. u. Biologie, no. 2: 1. See also Oak Ridge National Laboratory Translation (ORNL-tr-755).
28. Gentry, Robert V., T. J. Sworski, H. S. McKown, D. H. Smith, R. E. Eby, W. H. Cristie. 1982. Science 216: 296. See also R. V. Gentry. 1984. Science 223: 835.
29. Zartman, R. E. 1979. Los Alamos Sci. Lab. Rep. LA-7923-MS.
30. Gentry, R. V., G. Glish, & E. R. McBay. 1982. Geophys. Res. Lett. 9:1129.
31. Silk, J. 1979. The Big Bang. W. H. Freeman & Co., San Francisco.
32. Weinberg, S. 1972. Gravitation and Cosmology. Wiley, New York.
33. Hetherington, Norriss. 1971. Astron. Soc. of the Pacific, Leaflet No. 509, November.
34. Hawkins, G. S. 1962. Nature 194: 563.
35. Segal, I. E. 1976. Mathematical Cosmology and Extragalactic Astronomy. Academic Press. Idem. 1975. Proc. Nat. Acad. Sci. 72: 2473.
36. Nicoll, J. F. and I. E. Segal. 1975. Proc. Nat. Acad. Sci. 72: 4691.
37. Sandage, A., G. A. Tammann, and A. Yahil. 1979. Ap. J. 232: 352.
38. Nicoll, J. F. and I. E. Segal. 1982. Proc. Natl. Acad. Sci. 79: 3913. Idem. 1982. Ap. J. 258: 457. Idem. 1982. Astron. & Astrophys. 115: 398. See also Segal, I. E. 1982. Ap. J. 252: 37.
39. Nicoll, J. F. et al. 1980. Proc. Natl. Acad. Sci. 77: 6275.
40. Pound, R. V. and J. L. Snider. 1964. Phys. Rev. Lett. 13: 539. Idem. 1965. Phys. Rev. 140: B788.
41. Alley, C. 0. 1982. Proper Time Experiments in Gravitational Fields with Atomic Clocks, Aircraft, and Laser Light Pulses. In Quantum Optics, Experimental Gravitation, and Measurement Theory. Edited by P. Meystre and M. 0. Scully, Plenum Pub. Corp., New York.
42. North, J. D. 1965. The Measure of the Universe, Clarendon Press, Oxford.
43. Rastall, P. 1978. Astrophys. J. 22: 745. Idem. 1979. Can. J. Phys. 57: 944.
44. Marinov, S. 1981. Eppur Si Muove. East West Publishers, Graz, Austria.
45. Weisskopf, V. F. 1983. Am. Sci. 71, No. 5: 473.
46. Smoot, G. F. et al. 1977. Phys. Rev. Lett. 39: 898. Idem. 1979. Ap. J. 234: L83.
47. Einstein, A. 1939. Ann. Math. 40: 922.
48. Burcev, P. 1968. Phys. Lett. 27A: 623.
49. Gentry, R. V. 1983. Bull. of the Am. Phys. Soc. 28: 30.
50. Landsberg, P. T. and D. A. Evans. 1979. Mathematical Cosmology. Clarendon Press, Oxford.
51. Gentry, R. V. 1983. Phys. Today 36, No. 11: 124.
52. Ellis, G.F.R. et al. 1978. Mon. Not. R. Astr.Soc. 184: 439.
53. Varshni, Y. P. 1976. Astrophys. Space Sci. 43: 3. 1977. Ibid. 51: 121.
54. Clube, S.V.M. 1980. Mon. Not. R. Astr. Soc. 193: 385. Idem. 1982. Proceedings of an International Colloquium on the Scientific Aspects of the Hipparcos Mission, Strasbourg, France (ESA SP-177).
55. Clube, S.V.M. et al. 1980. Comm. R. Observatory, Edinburgh, No. 383: 467.
56. Jaakkola, T., M. Moles & J. P. Vigier. 1979. Astr. Na. 300:229.
57. Holden, C. 1984. Science 223: 1274.
58. Gentry, Robert V. 1984. Creation's Tiny Mystery (to be published).